The ancient arts: Geometry
- 2 minutes read - 337 wordsOften attributed to Kepler is a statement of the nature of the following. I don’t seem to have a copy of the Mysterium Cosmographicum handy, so I’ll parrot what I found at goldennumber.net:
“Geometry has two great treasures: one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold; the second we may name a precious jewel.” –Johannes Kepler
I’ve always been a fan of Kepler since I was in Holland and studied 16th century science. As Sagan said, he was the last of the mathematical astrologer or the first astronomer. Either way, Kepler and his odd sense of mysticism or keen sense of science managed to produce some stunning insights about the way our cosmos works, about planetary motion, and about geometry. In the quote above he refers to the “Golden Number” or the “Golden Ratio”: phi. Kepler, and his work, for me have always been one of those historical oddities of that era where Western science looked to shake off the shackles of church dogma and mysticism and become, properly, science. More odd trivia for me to know. Until…
After having finished Trig I thought that I would like to take a look at some of the finer points of subtending space by line, so I purchased this very nice “Mathematical Toolkit” for drawing lines, arcs, etc. at the local Office Depot the other night.

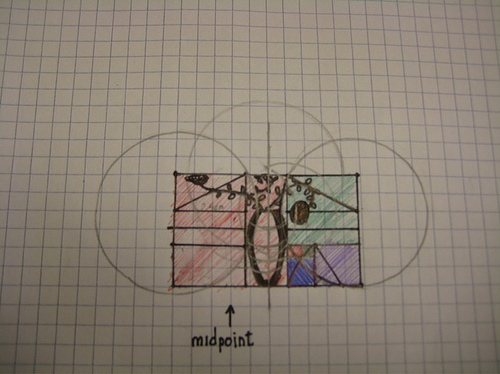
I haven’t really touched tools like these since early high school when I took Geometry, so it was a bit strange to reacquaint myself with their use. Figuring out how to create phi ratios, one of Kepler’s “treasures”, seemed like an obvious enough learning task. So I did. I shot pictures of the process and now share that process with you, Internet.
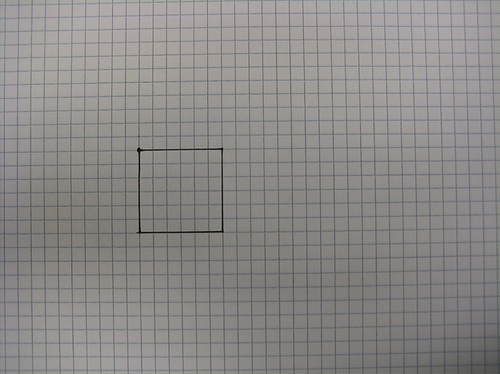
I pulled out some graph paper and made a square…
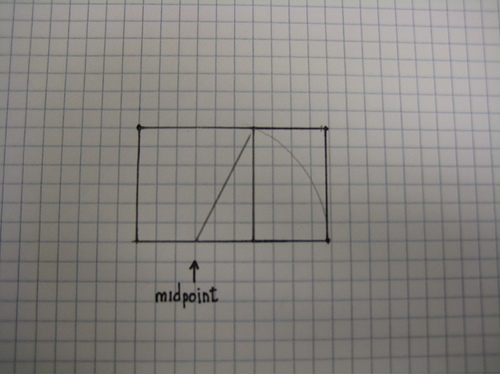
And made a golden rectangle from it…
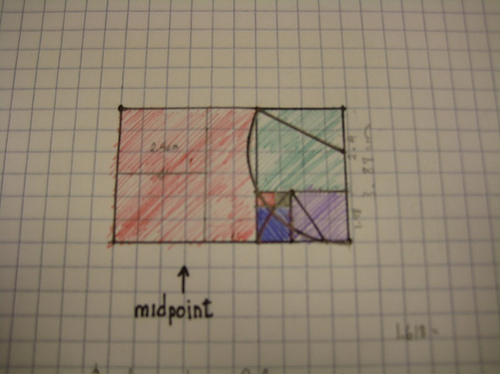
And many more from that one…
Maybe try to draw something in the space?